Convert 2.35 To A Fraction
Wondering how to catechumen decimals to fractions? Or how to convert fractions to decimals? It'due south easier than you think! Go along reading to encounter the steps for decimal to fraction conversions (including why y'all need to follow different steps if you accept a repeating decimal), steps for fraction to decimal conversions, a handy chart with common decimal/fraction conversions, and tips for quickly estimating conversions. How practise y'all convert a decimal to a fraction? Any decimal, even complicated-looking ones, can be converted to a fraction; you lot just need to follow a few steps. Beneath we explicate how to catechumen both terminating decimals and repeating decimals to fractions. A terminating decimal is whatsoever decimal that has a finite other of digits. In other words, information technology has an cease. Examples include .5, .234, .864721, etc. Terminating decimals are the virtually common decimals y'all'll see and, fortunately, they are besides the easiest to convert to fractions. Write the decimal divided past one. For case, say you lot're given the decimal .55.Your commencement step is to write out the decimal and then it looks similar ${.55}/{one}$. Next, you want to multiply both the elevation and lesser of your new fraction by 10 for every digit to the left of the decimal point. In our example, .55 has two digits after the decimal signal, then we'll want to multiply the entire fraction by 10 x 10, or 100. Multiplying the fraction past ${100}/{100}$ gives us ${55}/{100}$. The final step is reducing the fraction to its simplest form. The simplest form of the fraction is when the superlative and bottom of the fraction are the smallest whole numbers they can be. For example, the fraction ${3}/{nine}$ isn't in its simplest class because information technology can still be reduced downwards to ⅓ by dividing both the top and bottom of the fraction past 3. The fraction ${55}/{100}$ tin be reduced by dividing both the elevation and bottom of the fraction by 5, giving us ${11}/{20}$. 11 is a prime number number and tin can't exist divided any more, so we know this is the fraction in its simplest course. The decimal .55 is equal to the fraction ${11}/{20}$. Convert .108 to a fraction. Subsequently putting the decimal over i, nosotros terminate upwards with ${.108}/{1}$. Since .108 has 3 digits after the decimal place, we need to multiply the entire fraction by 10 x 10 x ten, or g. This gives us ${108}/{chiliad}$. Now we need to simplify. Since 108 and g are both even numbers, we know we can carve up both by 2. This gives united states ${54}/{500}$. These are however even numbers, so nosotros tin divide by two once more to get ${27}/{250}$. 27 isn't a factor of 250, so the fraction tin can't be reduced any more. The final reply is ${27}/{250}$. A repeating decimal is one that has no end. Since you tin can't keep writing or typing the decimal out forever, they are frequently written as a cord of digits rounded off (.666666667) or with a bar above the repeating digit(s) $\ov {(.6)}$. For our example, we'll convert .6667 to a fraction. The decimal .6667 is equal to $\ov {(.half-dozen)}$, .666666667, .667, etc. They're all just unlike means to show that the decimal is actually a string of half dozen'southward that goes on forever. Permit 10 equal the repeating decimal you're trying to convert, and place the repeating digit(s). So x=.6667 6 is the repeating digit, and the end of the decimal has been rounded up. Multiply by any value of 10 y'all demand to get the repeating digit(s) on the left side of the decimal. For .6667, we know that 6 is the repeating digit. We want that vi on the left side of the decimal, which ways moving the decimal place over i spot. Then we multiply both sides of the equation past (10 10 1) or 10. 10x = 6.667 Annotation: You only want one "ready" of repeating digit(s) on the left side of the decimal. In this example, with 6 as the repeating digit, you merely want one half dozen on the left of the decimal. If the decimal was 0.58585858, you lot'd just want one set of "58" on the left side. If it helps, you can picture all repeating decimals with the infinity bar over them, so .6667 would be$\ov {(.6)}$. Next nosotros want to get an equation where the repeating digit is only to the right of the decimal. Looking at x = .6667, we tin can see that the repeating digit (6) is already just to the right of the decimal, then we don't need to do whatever multiplication. We'll keep this equation equally x = .6667 At present we need to solve for 10 using our two equations, x = .667 and 10x = 6.667. 10x - x =6.667-.667 9x = 6 x = ${half dozen}/{9}$ 10 = ⅔ Catechumen 1.0363636 to a fraction. This question is a scrap trickier, but we'll be doing the aforementioned steps that we did above. First, make the decimal equal to x, and decide the repeating digit(s). 10 = 1.0363636 and the repeating digits are 3 and 6 Next, become the repeating digits on the left side of the decimal (again, you lot only want i prepare of repeating digits on the left). This involves moving the decimal iii places to the right, so both sides need to be multiplied past (ten x 3) or yard. 1000x = 1036.363636 Now become the repeating digits to the right of the decimal. Looking at the equation ten = 1.0363636, you tin can see that there currently is a zero between the decimal and the repeating digits. The decimal needs to be moved over one space, so both sides demand to be multiplied by 10 x i. 10x = 10.363636 At present use the two equations, 1000x = 1036.363636 and 10x = x.363636, to solve for 10. 1000x - 10x = 1036.363636 - 10.363636 990x = 1026 x = ${1026}/{990}$ Since the numerator is larger than the denominator, this is known as an irregular fraction. Sometimes you can leave the fraction as an irregular fraction, or you may be asked to convert information technology to a regular fraction. You can do this by subtracting 990/990 from the fraction and making information technology a 1 that'll go next to the fraction. ${1026}/{990}$ - ${990}/{990}$ = i ${36}/{990}$ x = one ${36}/{990}$ ${36}/{990}$ can exist simplified by dividing information technology by 18. x = 1 ${ii}/{55}$ The easiest way to catechumen a fraction to a decimal is just to utilize your calculator. The line between the numerator and denominator acts as a division line, so ${7}/{29}$ equals vii divided by 29 or .241. If y'all don't have access to a figurer though, you tin can still convert fractions to decimals by using long partitioning or getting the denominator to equal a multiple of 10. We explain both these methods in this section. Catechumen ${3}/{8}$ to a decimal. Here is what ${3}/{8}$ looks like worked out with long partitioning. ⅜ converted to a decimal is .375 Convert ${3}/{8}$ to a decimal. We want the denominator, in this case viii, to equal a value of 10. We can do this by multiplying the fraction by 125, giving us ${375}/{1000}$. Next we want to get the denominator to equal 1 then we tin can get rid of the fraction. We'll do this past dividing each part of the fraction by thou, which means moving the decimal over three places to the left. This gives us ${.375}/{ane}$ or just .375, which is our answer. Note that this method only works for a fraction with a denominator that tin easily exist multiplied to be a value of 10. However, there is a trick you can apply to judge the value of fractions y'all tin can't convert using this method. Bank check out the example below. Convert ⅔ to a decimal. At that place is no number you tin can multiply 3 by to make it an verbal multiple of ten, just you lot tin become shut. By multiplying ⅔ by ${333}/{333}$, nosotros get ${666}/{999}$. 999 is very shut to 1000, so let's human action similar it actually is 1000, split up each part of the fraction by 1000, and motion the decimal place of 666 three places to the left, giving us .666 The exact decimal conversion of ⅔ is the repeating decimal .6666667, but .666 gets usa very close. So whenever yous have a fraction whose denominator can't easily be multiplied to a value of ten (this volition happen to all fractions that convert to repeating decimals), only get the denominator equally close to a multiple of 10 as possible for a shut estimate. Below is a chart with common decimal to fraction conversions. Y'all don't need to memorize these, but knowing at least some of them off the tiptop of your head will brand it easy to do some common conversions. If you're trying to convert a decimal or fraction and don't have a computer, yous can likewise see which value in this nautical chart the number is closest to then you can make an educated guess of the conversion. Decimal Fraction 0.03125 ${i}/{32}$ 0.0625 ${1}/{sixteen}$ 0.1 ${1}/{10}$ 0.1111 ${1}/{nine}$ 0.125 ${ane}/{eight}$ 0.16667 ${1}/{6}$ 0.two ${one}/{5}$ 0.2222 ${2}/{9}$ 0.25 ${one}/{four}$ 0.three ${3}/{10}$ 0.3333 ${i}/{3}$ 0.375 ${3}/{8}$ 0.4 ${2}/{v}$ 0.4444 ${4}/{9}$ 0.v ${1}/{2}$ 0.5555 ${5}/{9}$ 0.six ${3}/{5}$ 0.625 ${5}/{8}$ 0.6666 ${2}/{3}$ 0.7 ${7}/{10}$ 0.75 ${3}/{4}$ 0.7777 ${7}/{9}$ 0.viii ${4}/{five}$ 0.8333 ${five}/{6}$ 0.875 ${vii}/{eight}$ 0.8888 ${8}/{9}$ 0.9 ${9}/{10}$ If you lot're trying to convert a decimal to fraction, first you need to determine if it's a terminal decimal (i with an end) or a repeating decimal (one with a digit or digit that repeats to infinity). Once yous've done that, yous can follow a few steps for the decimal to fraction conversion and for writing decimals as fractions. If you're trying to convert a fraction to decimal, the easiest way is just to apply your estimator. If you don't take one handy, you tin use long partitioning or get the denominator equal to a multiple of ten, then motion the decimal identify of the numerator over. For quick estimates of decimal to fraction conversions (or vice versa), you can look at our chart of common conversions and run across which is closest to your effigy to go a ballpark idea of its conversion value. Desire to know the fastest and easiest ways to convert between Fahrenheit and Celsius? We've got you covered! Check out our guide to the all-time ways to convert Celsius to Fahrenheit (or vice versa). Are you learning about logarithms and natural logs in math class?We have a guide on all the natural log rules you demand to know. Did you know that water has a very special density? Cheque out our guide to learn what the density of water is and how the density can change. Demand more than help with this topic? Bank check out Tutorbase! Our vetted tutor database includes a range of experienced educators who can help you polish an essay for English or explicate how derivatives work for Calculus. You tin can apply dozens of filters and search criteria to find the perfect person for your needs. 
How to Convert Decimals to Fractions
Converting a Terminating Decimal to a Fraction
Step 1
Footstep 2
Step 3
Example

Converting a Repeating Decimal to a Fraction
Step 1
Pace 2
Footstep 3
Stride iv
Example
How to Convert Fractions to Decimals
Long Division Method
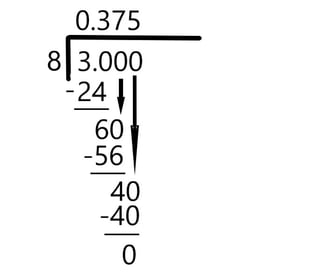
Denominator every bit a Value of ten Method
Step 1
Pace 2
Example
Common Decimal to Fraction Conversions
Summary: How to Brand a Decimal Into a Fraction
What'south Next?


About the Author
Christine graduated from Michigan State University with degrees in Environmental Biological science and Geography and received her Master'due south from Duke University. In high school she scored in the 99th percentile on the SAT and was named a National Merit Finalist. She has taught English and biological science in several countries.
Convert 2.35 To A Fraction,
Source: https://blog.prepscholar.com/convert-decimal-to-fraction
Posted by: geerdinduch.blogspot.com


0 Response to "Convert 2.35 To A Fraction"
Post a Comment